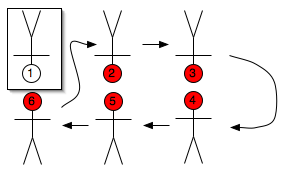
Figure 1: a six-person hug line. Person 1's partners are 6, 4, and 2, and then the cycle repeats. Partners of 1 are shown in red.
A group activity requires that a number of people partner with each other to hug, talk, or otherwise interact. The goal is that every person interacts with every other person. This is typically done with an even number of people so that nobody is left out.
This is a common situation for activities I've done at Unitarian Universalist retreats. Perhaps the most common situation is at the end of retreats as a way for everyone to say good-bye to everyone else. As this tends to be a situation where hugs are more appropriate than handshakes, this is known as a "hug line." This is hardly the only time that this occurs; getting-to-know-you activites and worship activities also frequently require this kind of mixing.
With an even number of people, the obvious (and easy) permutation strategy is for each person to choose the next partner my moving one position to the left. Unfortunately, as you move left, your partner also moves left, so partners switch by twos-- skipping every other person. Thus when you get back to your original partner, you've only faced half the people.
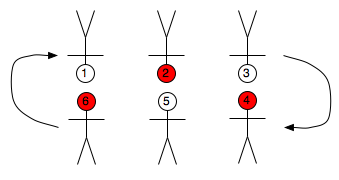
To illustrate this, number the people in a hug line. With a 6-person hug line, person 1 initially faces person 6. When they rotate, 1 moves to 2's position while 4 moves to 5's position. Thus, 1 faces 4, skipping 5. The entire rotation cycle for 1 is 6, 4, and 2. Odd-numbered people always face even numbered people, and vice-versa. This pattern remains true for any size group, so long as it is an even number of people.

With an odd number of people it is possible to break this cycle by having one person sit out each turn. The permutation is perfect: every person partners with every other person. The disadvantage is that one person is always lonely. This may be the best way to do hug lines with an odd number of people.
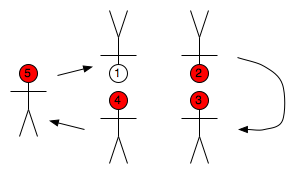
If you have an even number of people, rotate as normal except that one person remains fixed. This is identical to the lonely solution except that instead of having a person sit out, that person partners with the fixed person. This meets all of the goals of the hug line: it's simple enough to communicate to a large group, everybody is always engaged, and everybody pairs up with everybody else.